MetricsWeighted

Overview

{MetricsWeighted} provides weighted versions of different machine learning metrics and performance measures.

They all take at least four arguments:

actual: Actual observed values.
predicted: Predicted values.
w: Optional vector with case weights.
...: Further arguments.

Installation

# From CRAN
install.packages("MetricsWeighted")

# Development version
devtools::install_github("mayer79/MetricsWeighted")

Usage

Regression

library(MetricsWeighted)

# The data
y_num <- iris[["Sepal.Length"]]
fit_num <- lm(Sepal.Length ~ ., data = iris)
pred_num <- fit_num$fitted
weights <- seq_len(nrow(iris))

# Performance metrics
rmse(y_num, pred_num)
#> [1] 0.300627
rmse(y_num, pred_num, w = rep(1, length(y_num)))  # same
#> [1] 0.300627
rmse(y_num, pred_num, w = weights)                # different
#> [1] 0.3138009
mae(y_num, pred_num)
#> [1] 0.2428628
medae(y_num, pred_num, w = weights)
#> [1] 0.2381186

# MSE = mean normal deviance = mean Tweedie deviance with p = 0
mse(y_num, pred_num)
#> [1] 0.09037657
deviance_normal(y_num, pred_num)
#> [1] 0.09037657
deviance_tweedie(y_num, pred_num, tweedie_p = 0)
#> [1] 0.09037657

# Mean Poisson deviance equals mean Tweedie deviance with parameter 1
deviance_poisson(y_num, pred_num)
#> [1] 0.01531595
deviance_tweedie(y_num, pred_num, tweedie_p = 1)
#> [1] 0.01531595

# Mean Gamma deviance equals mean Tweedie deviance with parameter 2
deviance_gamma(y_num, pred_num)
#> [1] 0.002633186
deviance_tweedie(y_num, pred_num, tweedie_p = 2)
#> [1] 0.002633186

Binary classification

# The data
y_cat <- iris[["Species"]] == "setosa"
fit_cat <- glm(y_cat ~ Sepal.Length, data = iris, family = binomial())
pred_cat <- predict(fit_cat, type = "response")

# Performance metrics
AUC(y_cat, pred_cat)                 # unweighted
#> [1] 0.9586
AUC(y_cat, pred_cat, w = weights)    # weighted
#> [1] 0.9629734
logLoss(y_cat, pred_cat)             # Log loss = binary cross-entropy
#> [1] 0.2394547
deviance_bernoulli(y_cat, pred_cat)  # Log Loss * 2
#> [1] 0.4789093

Generalized R-squared

Furthermore, we provide a generalization of R-squared, defined as the proportion of deviance explained, i.e., one minus the ratio of residual deviance and intercept-only deviance, see (Cohen 2003).

For out-of-sample calculations, the null deviance is ideally calculated from the average in the training data. This can be controlled by setting reference_mean to the (possibly weighted) average in the training data.

summary(fit_num)$r.squared
#> [1] 0.8673123

# Same
r_squared(y_num, pred_num)
#> [1] 0.8673123
r_squared(y_num, pred_num, deviance_function = deviance_tweedie, tweedie_p = 0)
#> [1] 0.8673123

Pipe

In order to facilitate the use of these metrics with the pipe, use the function performance(): Starting from a data set with actual and predicted values (and optional case weights), it calculates one or more metrics. The resulting values are returned as a data.frame.

library(dplyr)

fit_num <- lm(Sepal.Length ~ ., data = iris)

# Regression with `Sepal.Length` as response
iris %>% 
  mutate(pred = predict(fit_num, data = .)) %>% 
  performance("Sepal.Length", "pred")
  
>  metric    value
>    rmse 0.300627

# Multiple measures
iris %>% 
  mutate(pred = predict(fit_num, data = .)) %>% 
  performance(
    "Sepal.Length", 
    "pred", 
    metrics = list(rmse = rmse, mae = mae, `R-squared` = r_squared)
  )

>    metric     value
>      rmse 0.3006270
>       mae 0.2428628
> R-squared 0.8673123

Parametrized scoring functions

Some scoring functions depend on a further parameter $p$ :

tweedie_deviance(): depends on tweedie_p.
elementary_score_expectile(), elementary_score_quantile(): depend on theta.
prop_within(): Depends on tol.

It might be of key relevance to evaluate such function for varying $p$ . That is where the function multi_metric() shines.

ir <- iris
ir$pred <- predict(fit_num, data = ir)

# Create multiple Tweedie deviance functions
multi_Tweedie <- multi_metric(deviance_tweedie, tweedie_p = c(0, seq(1, 3, by = 0.2)))
perf <- performance(
  ir, 
  actual = "Sepal.Length", 
  predicted = "pred",
  metrics = multi_Tweedie, 
  key = "Tweedie_p", 
  value = "deviance"
)
head(perf)
#>   Tweedie_p    deviance
#> 1         0 0.090376567
#> 2         1 0.015315945
#> 3       1.2 0.010757362
#> 4       1.4 0.007559956
#> 5       1.6 0.005316008
#> 6       1.8 0.003740296

# Deviance against p
plot(deviance ~ as.numeric(as.character(Tweedie_p)), data = perf, type = "s")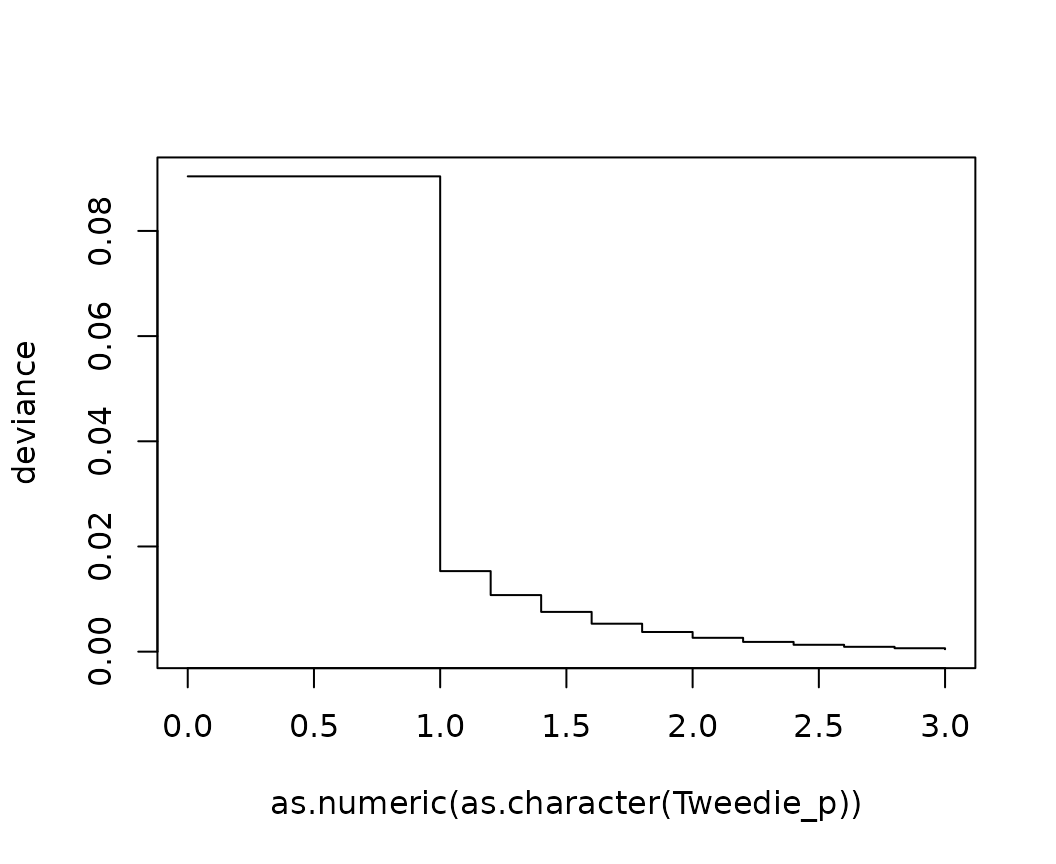

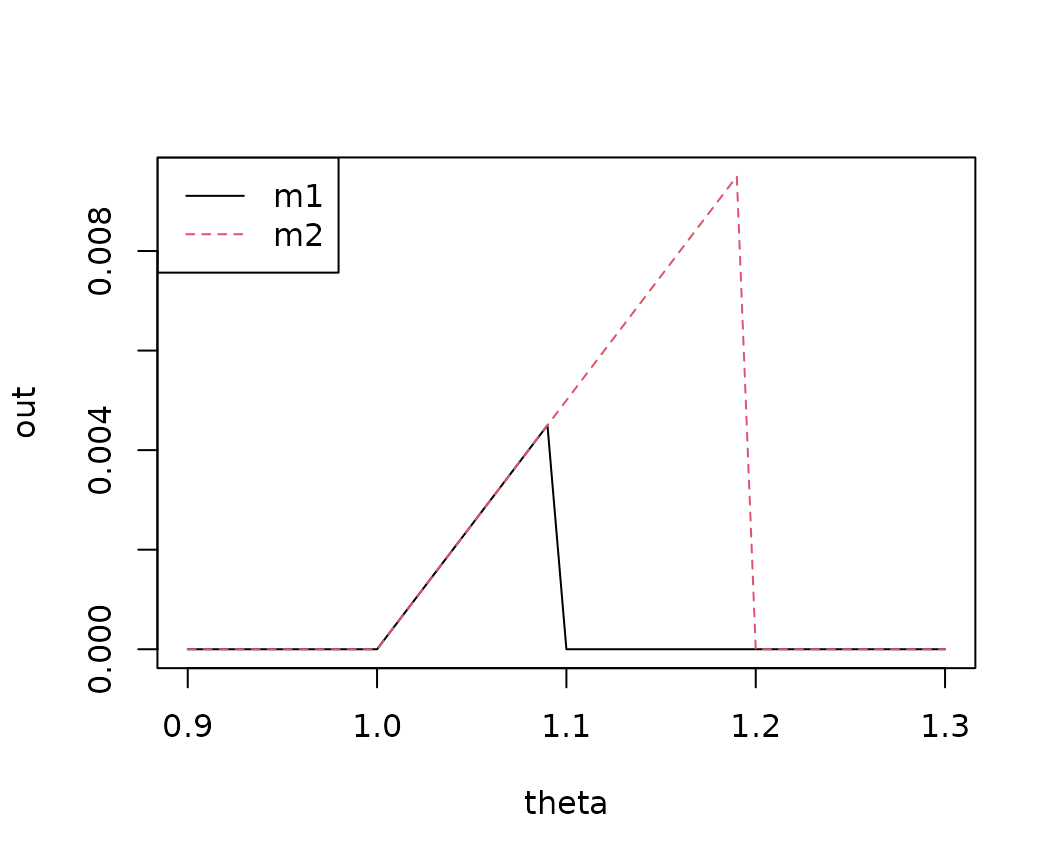
Murphy diagrams

The same logic as in the last example can be used to create so-called Murphy diagrams (Ehm et al. 2016). The function murphy_diagram() wraps above calls and allows to get elementary scores for one or multiple models across a range of theta values, see also R package murphydiagram.

y <- 1:10
two_models <- cbind(m1 = 1.1 * y, m2 = 1.2 * y)
murphy_diagram(y, two_models, theta = seq(0.9, 1.3, by = 0.01))

References

Cohen, Cohen, J. 2003. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. New York: Routledge. https://doi.org/10.4324/9780203774441.

Ehm, Werner, Tilmann Gneiting, Alexander Jordan, and Fabian Krüger. 2016. “Of Quantiles and Expectiles: Consistent Scoring Functions, Choquet Representations and Forecast Rankings.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 78 (3): 505–62. https://doi.org/10.1111/rssb.12154.

2024-07-30